6축 가속도/자이로 센서 개발 키트
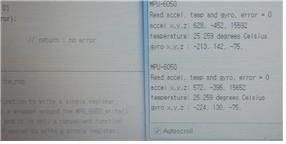
6축 가속도/자이로 센서 개발 키트입니다.
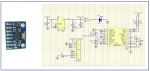
제품 구성 : MPU6050 가속도/자이로 센서 및 MCU 인터페이스 회로, MCU 및 구성 회로, PC 출력용 소프트웨어 알고리즘이 되겠습니다.
구매 연락처 : 010-4293-9577, e-mail : nano@nano-i.com 1. 실시간 출력 원시 데이터 (Krodal 코드) : 가속도 Ax, Ay, Az, 각속도 Wx, Wy, Wz, 현재 온도 입니다. (가속도 : 단위 시간당 속도의 변화량, 각속도 : 단위 시간당 각도의 변화량) 2. 아래는 MCU 칩에서 실시간 출력되는 원시 데이터를 사용하여 오일러각을 계산하여 동영상 이미지로 출력하는 과정을 나타내며, 즉 실시간의 가속도 및 각속도 데이터를 사용하여 공간상에서의 센서의 회전각을 가속도계와 자이로 센서 데이터를 융합한 보상 필터 방법에 의하여 표현한 프로그램 소스를 제공합니다.
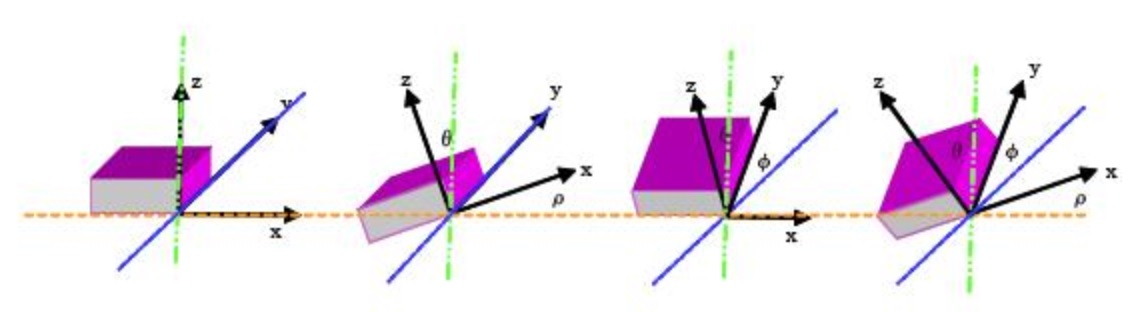
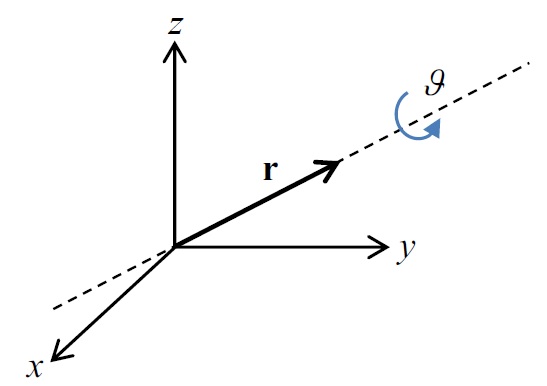
MPU-6050 데이터시트의 13페이지 (구매 시 같이 제공 예정) 에 의하면, Krodal 코드의 원시 가속도 데이터값을 16384 로 나누어 중력가속도 9.8 m/sec^2 을 곱하면 우리가 원하는 가속도 값을 얻어낼 수가 있습니다. 이 측정된 가속도 값을 가지고 센서의 회전 각도값으로 변환하는 것은 각 가속도 벡터 성분 비(ratio) 를 사용합니다. 즉, 회전각을 세 축으로 분해하여 표현할 수 있는데 (위키 백과의 오일러각 참조 : X 축 주위로 회전한 각도로 roll, Y 축 주위로 회전한 각도로 pitch, 그리고
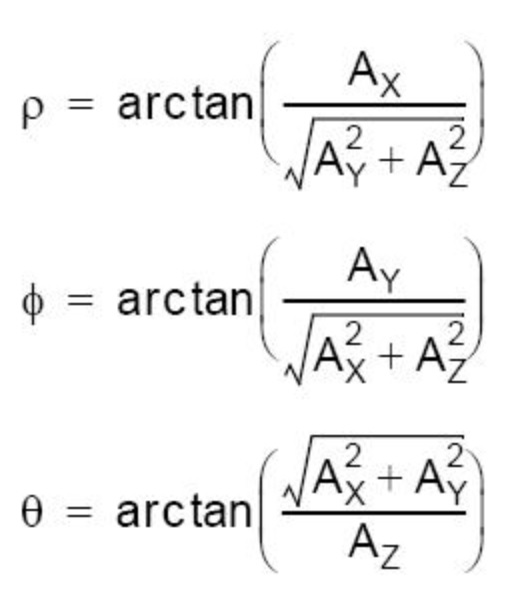
Z 축 주위로 회전한 각도로 yaw) , 이 측정 가속도 데이터를 가지고서는 X 축 주위로 회전한 각도 (φ) 와 Y 축 주위로 회전한 각도 (ρ) 를 계산할 수 있습니다. 순수한 가속도 값을 가지고 회전각을 나타낸다면 아래와 같이 표현되어집니다. 위 공식은 가속도 값을 가지고 회전각 또는 틸트각을 계산하는 방법을 나타냅니다. ρ 와 φ 값은 각각 X 축과 Y 축의 틸트값을 나타냅니다. 여기서, ρ 와 φ 값은 각각 Pitch 와 Roll 을 나타내고, θ 는 Z 축의 중력축에 대한 틸트 값을 나타내므로 Yaw 는 아닙니다. 그러므로 Yaw 는 가속도계로부터 계산할 수 없습니다. 그런데, 중력이 센서에 유일하게
가해지는 힘이라면 가속도계의 측정 결과는 정확한 방향각 (Orientation) 을 나타냅니다. 그러나 병진 운동과 회전 운동하는 센서의 경우, 센서에 힘을 가해주어야 하므로
측정값의 요동을 초래합니다. 가속도값 데이터는 간단하지만 심각한 요동으로 노이즈를 상당히 타는 경향이 있습니다. 만약에 이 값들을 평균해서 산출해낼 수 있다면
가속도계는 요동의 시간보다 긴 시간 동안의 그것을 나타낼 것이므로 정확한 측정값을 제공할 것입니다.
자이로 센서로부터
방향각(Orientation) 을 계산하는 방식은 다른데, 왜냐하면 자이로센서는 방향각 자체라기 보다는 각속도 (단위 시간당 방향각의 변화) 를 측정하기 때문입니다. 방향각을
계산하기 위해서는 센서의 위치를 처음부터 알고 있는 방향 (가속도계로부터 가능) 으로 초기화해야 하고, 그 다음에는 어느 시간 동안(Δt) X, Y, 그리고 Z 축 주위를 회전하는 각속도(ω) 를 측정해야 합니다. 그러면, ω × Δt = 각도 변화량을 산출해냅니다. 산출된 방햑각은 원래의 각도에다가 이
변화량을 더한 값이 됩니다. 이러한 문제를 푸는 방법으로, 아주 작은 시간 동안의 각도 변화 값을 하나하나씩 다 더하는 이른 바 적분하는 방식으로
방향각을 계산해냅니다. ω × Δt 를 반복적으로 더하는 방식은 작은 구조적 오차를 초래합니다. 즉,
자이로스코프 드리프트 라는 것을 초래하는데, 그것은 긴 시간 동안의 자이로센서 데이터는 비정확도가 증가하는 것을 의미합니다.
MPU-6050 데이터시트에서는 자이로스코프의 원시 데이터를 131로 나누면
단위 초당 각도를 나타내는 각속도 값임을 보여주며, 측정 인터벌에서의 이 값에 시간을 곱하면
각도값으로 변환됨을 의미합니다. 만일 앞에서 측정한 각도 위치를 저장해두면 각 시간 동안에 새로운 계산값을
간단히 더해주는 방식으로 새로운 각도 값을 얻을 수 있습니다.
위에서 설명한 것과 같이, 가속도계와 자이로스코프 데이터 둘 다 구조적인 오차가 쉽게 발생함을 보여주고 있습니다. 가속도계는 긴 시간 동안의 정확한 데이터를 제공하지만, 짧은 시간
동안에는 노이즈가 발생합니다. 자이로스코프는 짧은 시간 동안의 정확한 방향각 변화를 보여주지만, 긴 시간 동안의 적분으로 인하여 드리프트가 발생합니다.
이러한 문제 해결 방안으로는 가속도계와 자이로스코프 데이터를 모두 혼용하는 방식으로 오차를 제거하는
방식이 되겠습니다. 이 두가지 데이터를 결합하는 방식이 바로 칼만필터
(Kalman filter) 라고 하는데 다소 복잡하긴 합니다. 다행히도 더 간단한 접근법이
있는데 바로 보상 필터 (Complementary filter) 방식이라고 합니다.. 다음은 가속도계와 자이로스코프 데이터를 융합한 공식입니다.
보상각도 = α × (자이로스코프 각도) + (1 - α) × (가속도계 각도)
여기서, α = τ/(τ + Δt) 이고 , (자이로스코프 각도) = (최근 측정된 보상각) + ω×Δt
Δt = 샘플링 레이트
(sampling rate), τ = 일반적으로 가속도 노이즈의 소요시간 보다 긴 시간을 의미하는
시간 상수.
여기서 샘플링 레이트를 0.04 초로 두고 시간 상수를 1 초로 두어서 α ≈ 0.96 를 부여하였습니다.
아래 동영상은 위의 공식을 사용하여
가속도/자이로 센서의 실시간 회전각을 사용한 동영상 궤적을 표현하였습니다.
위의 1번 항목의 MCU 용 원시 프로그램 소스와 함께, 아래의 영상은 제공되어지는 보상 필터를 사용한 프로그램 소스를 사용한 실행 영상입니다. 동영상 설명
참조 바랍니다.
3. 다음은 오일러 각을 사용함으로 발생하는 짐벌락 (Gimbal lock) 문제를 피하고 360 전방위에 대한 회전각을 구하는
quaternoins 방법을 사용한 결과입니다.
위에서 pitch, roll, 그리고 yaw (오일러
각이라고 알려졌으며, 각각 X ,Y ,그리고 Z 축을 중심으로 회전한 각도) 값을 계산하여 얻었습니다. 이들 계산값에 대하여 가속도계와 자이로스코프의 특성으로 인하여 제한 조건이 있습니다.
그것은 자이스코프 데이터는 시간에 따라 드리프트되는 경향이 있고, 가속도 데이터는 노이즈가 있고 180 도 이상의 각도에서는 회전각을 계산하기 어려운 것입니다. 아래는 각속도계의
측정값으로부터
계산되어진 roll 과 pitch 값을 나타내고 있습니다. 또한, yaw 값은
가속도계로부터 계산될 수 없습니다.
아래는 각속도계의 측정값 (Ax, Ay, Az ) 로부터
계산되어진 roll ( φ ) 와 pitch ( ρ ) 값을 나타내고 있습니다. (또한 yaw 값은
가속도계로부터 계산될 수 없습니다.)
Arctan 함수의 범위는 { -π/2, π/2 } 이고, 이 함수를 사용하여 운동각의 범위를 쉽게 결정할 수 있습니다. 추가적으로
회전각 계산을 위하여 오일러 각을 사용할 때 짐벌락 (Gimbal lock) 이라는 문제에 직면하게
됩니다. 오일각 회전은 순차적으로 (예를 들면 roll, pitch, 그 다음은 yaw) 이루어지기 때문에, 두 번째 회전각이 90 도 각도에 근접하였을 때 문제는 발생합니다. 왜냐하면 이것은 첫 번째와 세 번째 회전축이 한 평면상에서 서로 얼라인이 되기 때문입니다. 이것을 우리는 짐벌락 (Gimbal Lock) 이라고 합니다. 그러므로 여기서 회전축에 대한 자유도가 하나 줄어들게 됩니다. 회전 순서를 바꾸어 표현하면 짐벌락 현상이 없어집니다. 그러나 회전 운동을 표현하는 동안 역시 짐벌락 현상이 다시 발생하게 되고, 회전 순서를 또 한 번 바꾸는 방법을
사용하게 됩니다.
다음 영상은 오일러각과 짐벌락 현상에 대하여 잘 설명해주고 있습니다.
그러므로 짐벌락 현상을 없애기 위하여 등장한 원리가 사원수(Quaternion) 입니다. Quaternion은 19세기에 윌리엄 해밀턴(William Rowan Hamilton)에 의해 발견되었습니다. 오일러 각의 회전 행렬은 9개의 원소로 표현할 수 있는 반면에, 사원수는 4개의 원소로 간결하게 표현할 수가 있습니다.
사원수는 3개의 벡터 요소과 한 개의 스칼라 요소로 구성되어집니다. 표현하자면,
입니다. 여기서 η 는 쿼터니언의 스칼라 성분이고,
는 쿼터니언의 벡터 성분입니다.
위와 같이 물체의 회전을 규정하는데 있어서 간단히 네개의 쿼터니언 값을 사용합니다. 이러한 이 중 세 개는 X,Y,Z 공간좌표축에 대한 벡터량을 정의하고, 나머지 하나는 회전에 대한 스칼라 양을 정의합니다.
이
방법은 수학적으로 표현하는데 있어서 다소 복잡하므로 여기서는 배제하겠습니다. Quaternions 방법은 짐벌락 문제를 피하고 어렵지 않게 180 도 이상의 각을 표현할 수 있습니다. 제공되어지는 DMP에 저장된 알고리즘에는 유용한 수학적인
특성들이 있는데, 그것은 애니메이션에 유용하도록 두 쿼터리온 사이에 직접적인 해석을 허락하고, 겹겹의 회전 오페레이션을 순자적으로 시행할 때의 round-off 오차를 줄이는 것입니다.
즉, MPU6050
IMU 센서에는 DMP (Digital Motion Processor)가 있는데, 그것은
가속도와 자이로 센서 데이터를 융합하여 각 센서에 대한 고유 에러를 최소화합니다. DMP 는 쿼터니온으로
결과를 계산하여 오일러 각으로 변환할 수 있습니다. 또한 다른 계산도 가능합니다.
당사는 DMP
로부터
데이터를 추출해내는 유용한 라이브러리 함수도 제공합니다. 이 라이브러리 함수 파일을 지정된 폴더에 저장하시면
되겠습니다.
또한 제공되는 MCU 칩에 저장되는 쿼터니언을 사용하여 오일러각으로 변환되어 컴퓨터로 데이터를 통신되는 원시 파일과 아래 동영상과 같이 컴퓨터에서 가속도/자이로 센서의 각도 궤적을 볼 수 있는 개발용 소프트웨어 소스도 제공합니다.
위 비디오의 3차원 형태의 비행기와 화살표 그림은 현재 다루고 있는 IMU (Inertial Measurement Unit) 센서의 회전 상태를 나타내고 있습니다. 180 도 각도를 넘어선 상태에서도 임의의 각도에 대한 회전을
잘 표현해주고 있습니다. 처음에는 Yaw drift 가 몇
초간 있는데, 8 초 정도의 시간 이후에는 IMU 의 모션이
멈추면서 이 현상이 없어짐이 확인되어집니다. 이는 DMP 자체에서
캘리브레이션한 결과입니다. 앞에서 다룬 보상필터 방법으로도 roll 과 pitch 의 drift 에 대한 캘리브레이션이 가능하지만, yaw 에 대하여서는 불가능합니다. 또한 DPM 자체에서는 온도 보상을 하는 기능이 있으므로 주변 온도 변화에도 자체적으로 데이터 값이 보상값으로 출력됩니다.
이와 같이 MPU6050
IMU 센서의 Krodal 코드에 의한 가속도와 각속도에 대한 원시 데이터, 이를 사용하여 보상 필터 방법에 의한 오일러 각 표현, 짐벌락 현상을 피하고 정확하게 360 도 전 방위에 대하여 회전 궤적을 알 수 있는 쿼터니온법에 의한 회적각
표현 및 응용 기술을 개발할 수 있는 개발 키트를 제공하게 되었습니다. 응용 기술 개발도 연락을 기다리겠습니다. 감사합니다.
구매 연락처 : 010-4293-9577, e-mail : nano@nano-i.com 구매 사례 : 카메라 떨림 보정
장치용 (선박용 카메라) 응용 기술 개발 사례 : 몸동작
모션 캡쳐


![]()
![]()
![]()
![]()
-
원격 센서 모니터링 및 현장용 자료 저장 장치
-
스마트 카운터 개발키트
-
수중 초음파 통신 개발키트
-
차세대 IMU 개발 키트
-
360 도 스캔 라이다 개발키트 (확장 거리형, 제품 수명 5년)
-
짐벌락 없는 Yaw Pitch Roll 각도 출력 6축 자이로 센서 개발키트
-
드론의 고도 유지 및 지형 추적 또는 기타 응용의 TOF 방식의 라이다 (Lidar) 개발 키트
-
지자기 센서가 포함된 짐벌락이 없는 9축 자이로 센서 개발키트
-
지구의 자전과 공전이 보정된 짐벌락이 없는 6축 자이로 센서 개발키트
-
투명 마스크 (강의 행사 연예인용)
-
자율주행 미니 로봇 (Robot) 개발 키트
-
저류조 CBM 예측 진단 시스템
-
스스로 사고하는 학습에 의한 인공 지능 영상 분석 솔루션
-
휴대용 라이다 개발 키트 (모델 : A1)
-
수중 초음파 센서 개발 키트
-
휴대용 3D 스캐너 / 3D 프린터 융합 스타터 키트
-
선박 내 또는 주변 영상 센서 통합 관리 시스템
-
6축 가속도/자이로 센서 개발 키트
-
2차원 또는 3차원 레이저 가공용 스캐너 (독일제)
-
스마트폰에 부착하는 현미경 (어플 포함)
Designed by sketchbooks.co.kr / sketchbook5 board skin
Sketchbook5, 스케치북5
Sketchbook5, 스케치북5
Sketchbook5, 스케치북5
Sketchbook5, 스케치북5


 선박 내 또는 주변 영상 센서 통합 관리 시스템
선박 내 또는 주변 영상 센서 통합 관리 시스템